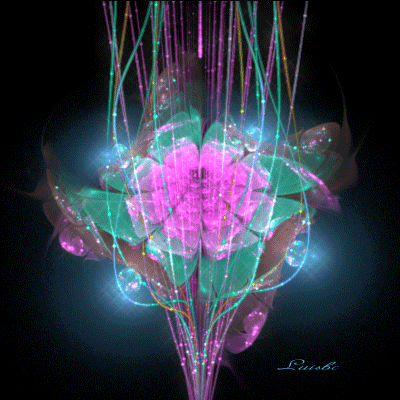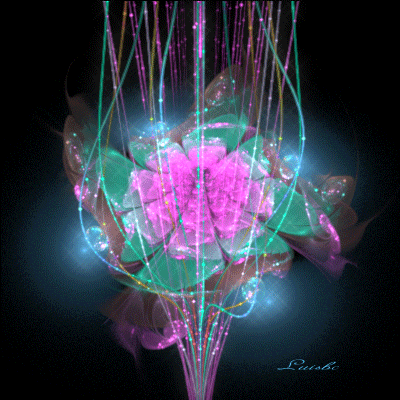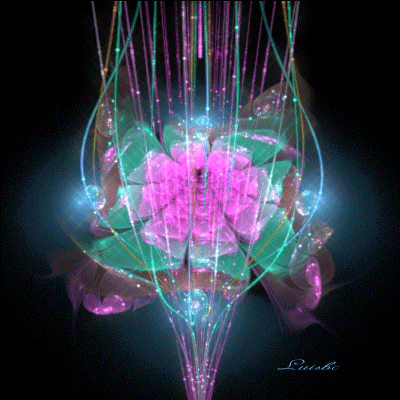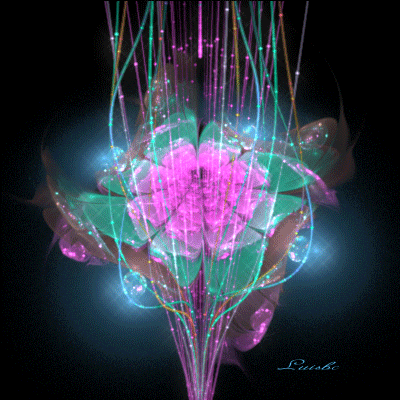
Относительно молодой и оригинальный вид искусства, создаваемый математическими формулами, завоевывает все больше поклонников. Для его создания не нужны ни рисунки ни фотографии, все проще и сложнее одновременно.

Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов. Слово фрактал образовано от латинского fractus и в переводе означает состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта `The Fractal Geometry of Nature'. В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему.

Роль фракталов в машинной графике сегодня достаточно велика. Они приходят на помощь, например, когда требуется, с помощью нескольких коэффициентов, задать линии и поверхности очень сложной формы. С точки зрения машинной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фактически найден способ легкого представления сложных неевклидовых объектов, образы которых весьма похожи на природные.

Одним из основных свойств фракталов является самоподобие. В самом простом случае небольшая часть фрактала содержит информацию о всем фрактале.

Определение фрактала, данное Мандельбротом, звучит так: "Фракталом называется структура, состоящая из частей, которые в каком-то смысле подобны целому"

Итальянка Сильвия Кордедда (Silvia Cordedda) создала целую серию работ, которую мы можем условно назвать «Несуществующие цветы и другие растения». Для того, чтобы было более понятно, суть фрактальных изображений, создаваемая математическими формулами, сводится к тому, что если мы увеличим мелкие объекты, то увидим в них повторения всей общей структуры. И так может продолжаться до бесконечности. Фрактальное искусство не ограничено изображениями. Это может быть анимация, 2D и 3D-графика, и даже музыка.



Источник

Фрактальные животные

Или их еще называют в интернете огненными животными.


Фрактал - это такая геометрическая фигура, в которой все элементы подобны друг другу. Чаще всего можно видеть фрактальное видео, когда камера приближается к определенной точке рисунка, а он при каждом приближении повторяется вновь и вновь. Этакое бесконечное путешествие внутри рисунка. Еще фрактал что-то там связан с метрической размерностью и нетривиальной структурой. Но, главное, это просто необычные и красочные картинки.



Источник